[알고리즘] 정렬 알고리즘

[알고리즘] 정렬 알고리즘

2022. 10. 7. 19:17ㆍCS/알고리즘

버블 정렬(Bubble sort)

개념

서로 인접한 두 원소를 검사하여 정렬하는 알고리즘, 인접한 두 개의 레코드를 비교하여 크기가 정렬되어 있지 않으면 서로 교환한다.

예시

초기 상태 배열 : 7, 4, 5, 1, 3

시간 복잡도

O(N^2)

선택 정렬(Selection sort)

개념

- 해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘

- 첫 번째 순서에는 첫 번째 위치에 가장 최솟값을 넣고, 두 번째 순서에는 두 번째 위치에 남은 값 중에서 가장 최솟값을 넣는다.

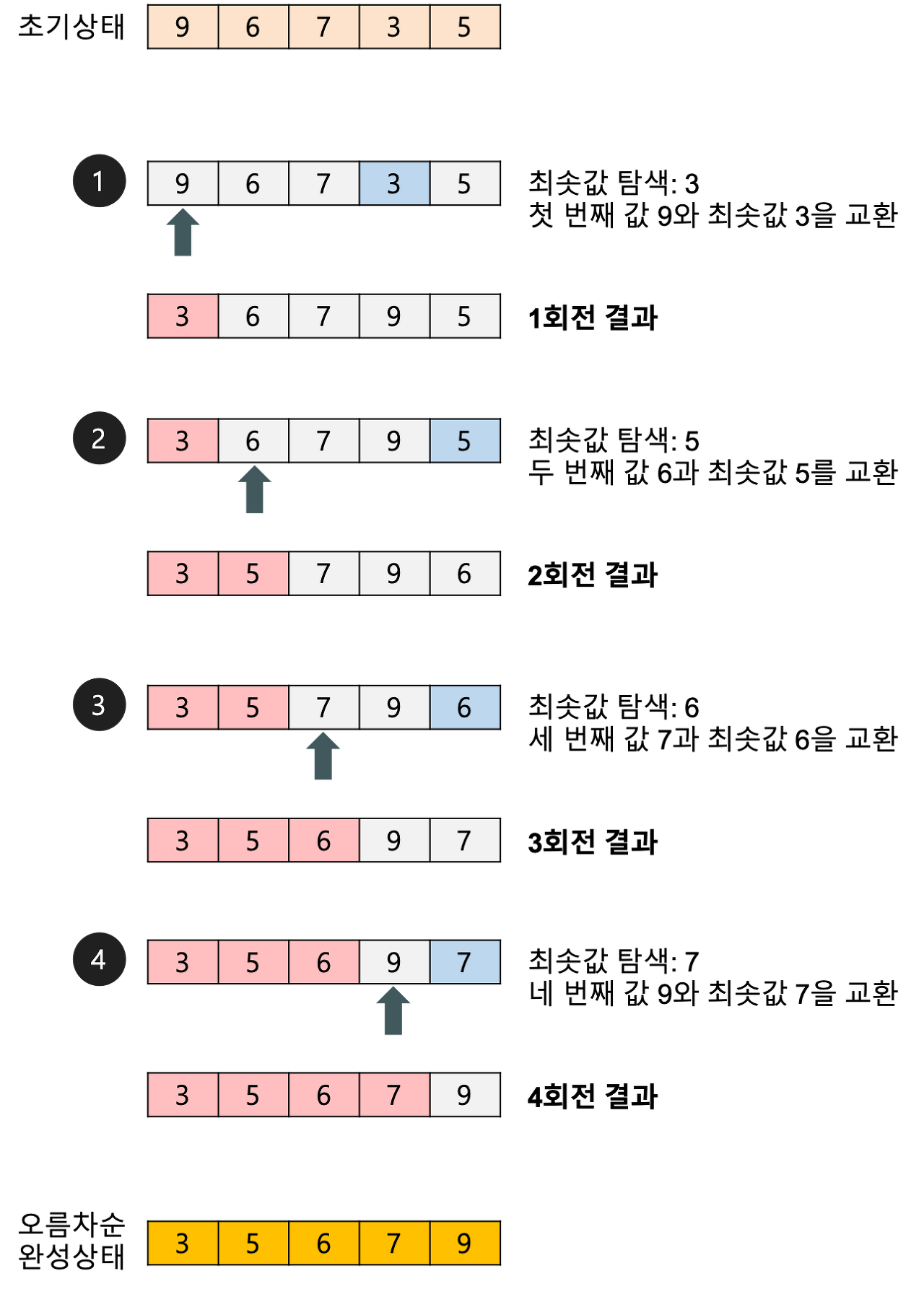
- 선택 정렬은 첫 번째 자료를 두 번째 자료부터 마지막 자료까지 차례대로 비교하여 가장 작은 값을 찾아 첫 번째에 놓고, 두 번째 자료를 세 번째 자료부터 마지막 자료까지와 차례대로 비교하여 그 중 가장 작은 값을 찾아 두 번째 위치에 놓는 과정을 반복하며 정렬 수행

- 1회전 수행하고 나면 가장 작은 값의 자료가 맨 앞으로 오게 됨

예시

시간복잡도

O(N^2)

삽입 정렬(Insertion sort)

개념

삽입 정렬 알고리즘 개념 요약
- 손 안의 카드를 정렬하는 방법과 유사함
  - 새로운 카드를 기존의 정렬된 카드 사이의 올바른 자리를 찾아 삽입
  - 새로 삽입될 카드의 수만큼 반복하게 되면 전체 카드가 정렬됨
- 자료 배열의 모든 요소를 앞에서부터 차럐대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘
- 매 순서마다 해당 원소를 삽입할 수 있는 위치를 찾아 해당 위치에 넣는다.
삽입 정렬 알고리즘의 구체적인 개념
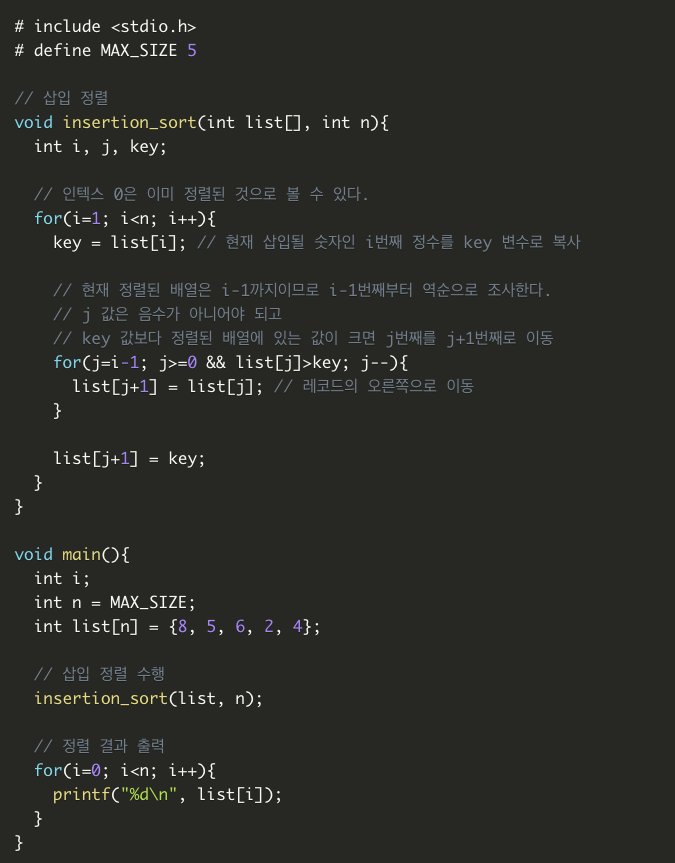
- 삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬하는 알고리즘
- 즉, 두 번째 자료는 첫 번째 자료,세 번째 자료는 두 번째와 첫 번째 자료...와 비교한 후 삽입될 위치를 찾음

예시

시간복잡도

O(N^2)

셸 정렬 (Shell sort)

개념

셸 정렬 알고리즘의 개념 요약
- 삽입 정렬을 보완한 알고리즘
- 삽입 정렬이 어느 정도 정렬된 배열에 대해서는 대단히 빠른것에 착안
- 삽입 정렬의 최대 문제점: 요소들이 삽입될 때, 이웃한 위치로만 이동
- 즉, 만약 삽입되어야 할 위치가 현재 위치에서 상당히 멀리 떨어진 곳이라면 많은 이동을 해야함
- 삽입 정렬과 다르게 셸 정렬은 전체의 리스트를 한 번에 정렬하지 않음
셸 정렬 알고리즘의 구체적인 개념
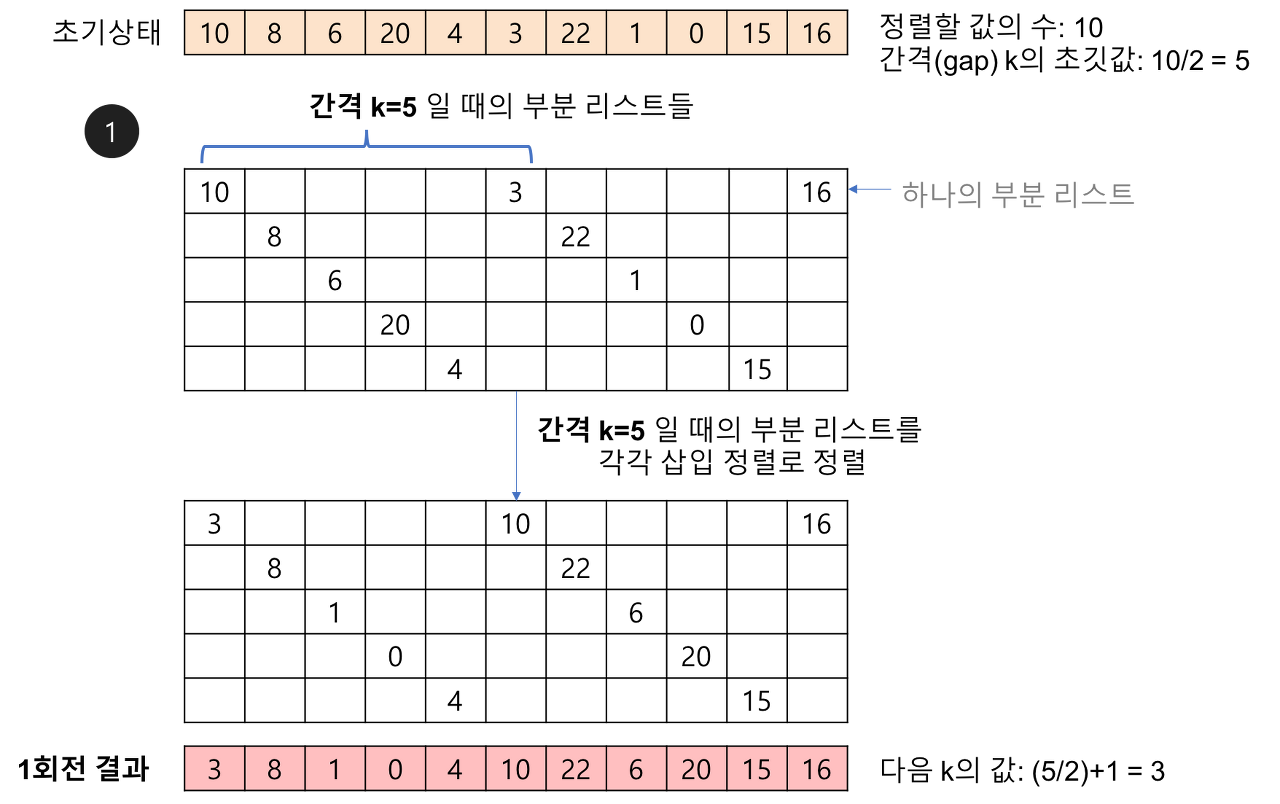
- 정렬해야 할 리스트의 각 k번째 요소를 추출해서 부분 리스트를 만든다. 이때 k를 '간격(gap)'이라 함
  - 간격의 초깃값 :(정렬할 값의 수)
  - 생성된 부분 리스트의 개수는 gap과 같음
- 각 회전마다 간격k를 절반으로 줄인다.
- 즉, 각 회전이 반복될 때마다 하나의 부분 리스트에 속한 값들의 개수는 증가함
  - 간격은 홀수로 하는 것이 좋음
  - 간격을 절반으로 줄일 때 짝수가 나오면 +1을 해서 홀수로 만듦

예시

# include <stdio.h>
# define MAX_SIZE 10

// gap만큼 떨어진 요소들을 삽입 정렬
// 정렬의 범위는 first에서 last까지
void inc_insertion_sort(int list[], int first, int last, int gap){
  int i, j, key;

  for(i=first+gap; i<=last; i=i+gap){
    key = list[i]; // 현재 삽입될 숫자인 i번째 정수를 key 변수로 복사

    // 현재 정렬된 배열은 i-gap까지이므로 i-gap번째부터 역순으로 조사한다.
    // j 값은 first 이상이어야 하고
    // key 값보다 정렬된 배열에 있는 값이 크면 j번째를 j+gap번째로 이동
    for(j=i-gap; j>=first && list[j]>key; j=j-gap){
      list[j+gap] = list[j]; // 레코드를 gap만큼 오른쪽으로 이동
    }

    list[j+gap] = key;
  }
}

시간복잡도

평균 O(N^1.5)

최악 O(N^2)

합병 정렬 (Merge sort)

개념

합병 정렬 알고리즘의 개념 요약
- 분할 정복 알고리즘의 하나
  - 분할 정복 방법
    - 문제를 작은 2개의 문제로 분리하고 각각 해결한 다음, 결과를 모아서 원래의 문제를 해결하려는 전략
    - 분할 정복 방법은 대개 순환 호출을 이용하여 구현함
합병 정렬 알고리즘의 구체적인 개념
- 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법
- 합병 정렬은 다음의 단계들로 이루어짐
  - 분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할
  - 정복(Conquer): 부분 배열을 정렬함. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용
  - 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병함
- 합병 정렬 과정
  - 추가적인 리스트가 필요
  - 각 부분 배열을 정렬할 때도 합병 정렬을 순환적으로 호출하여 적용
  - 합병 정렬에서 실제로 정렬이 이루어지는 시점은 2개의 리스트를 합병(merge)하는 단계

예시

시간복잡도

O(NlogN)

퀵 정렬 (Quick sort)

개념

퀵 정렬 알고리즘의 개념 요약
- 분할 정복 알고리즘의 하나로 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬방법
  - 합병 정렬과 달리 퀵 정렬은 리스트를 비균등하게 분할함
- 분할 정복 방법
  - 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아 원래의 문제를 해결하는 전략
  - 분할 정복 방법은 대개 순환 호출을 이용하여 구현
퀵 정렬 알고리즘의 구체적인 개념
- 하나의 리스트를 피벗(Pivot)을 기준으로 두 개의 비균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법
- 퀵 정렬은 다음의 단계들로 이뤄짐
  - 분할(Divide): 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)로 분할
  - 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용함
  - 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병함
  - 순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)은 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있음

예시

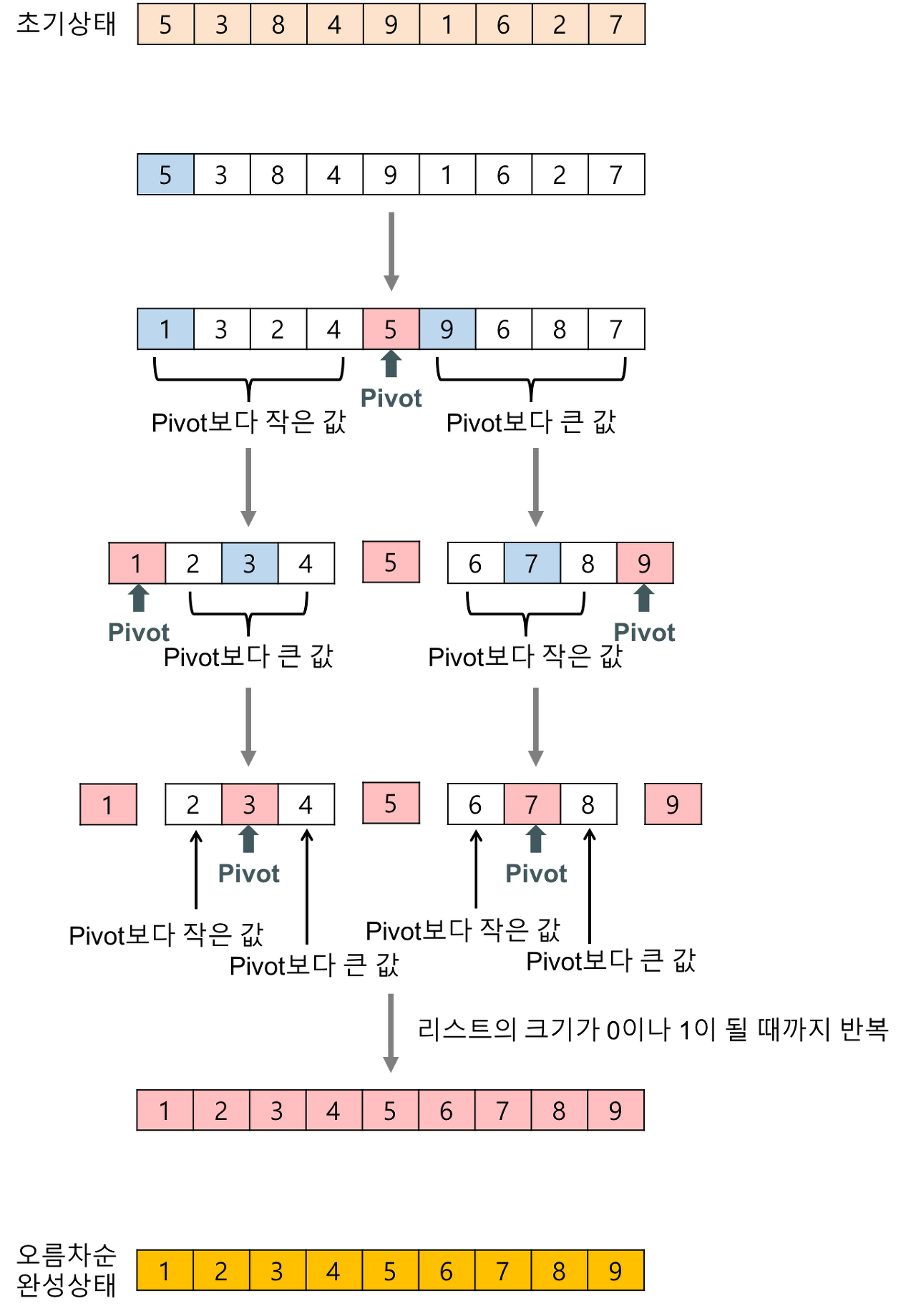
시간 복잡도

평균 O(NlogN)

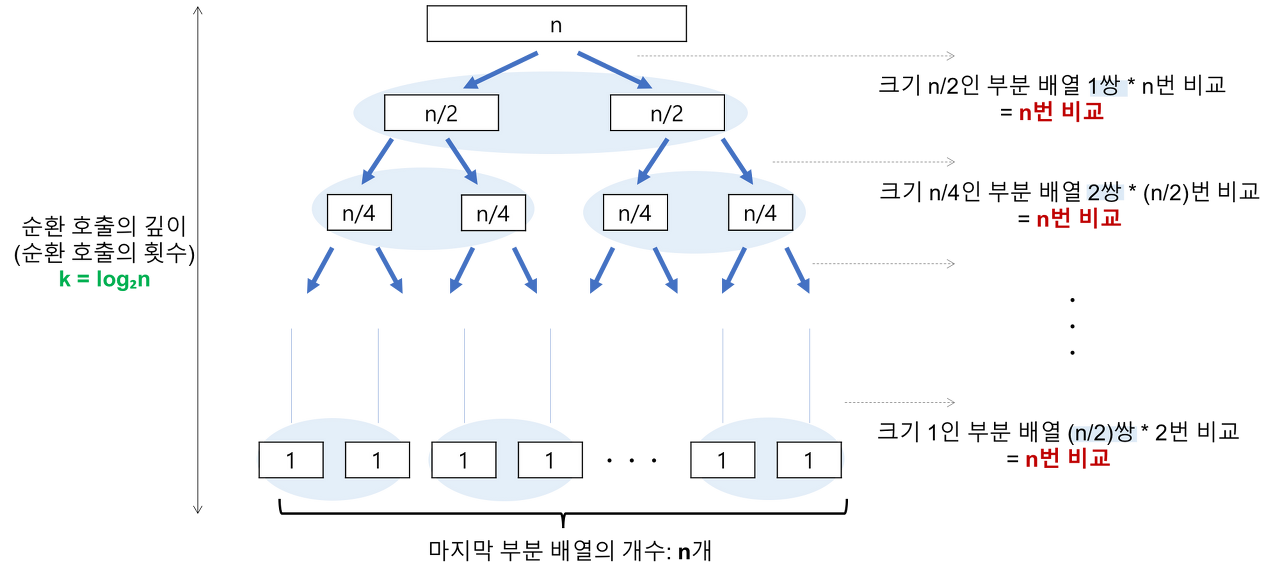
최악 O(N^2)

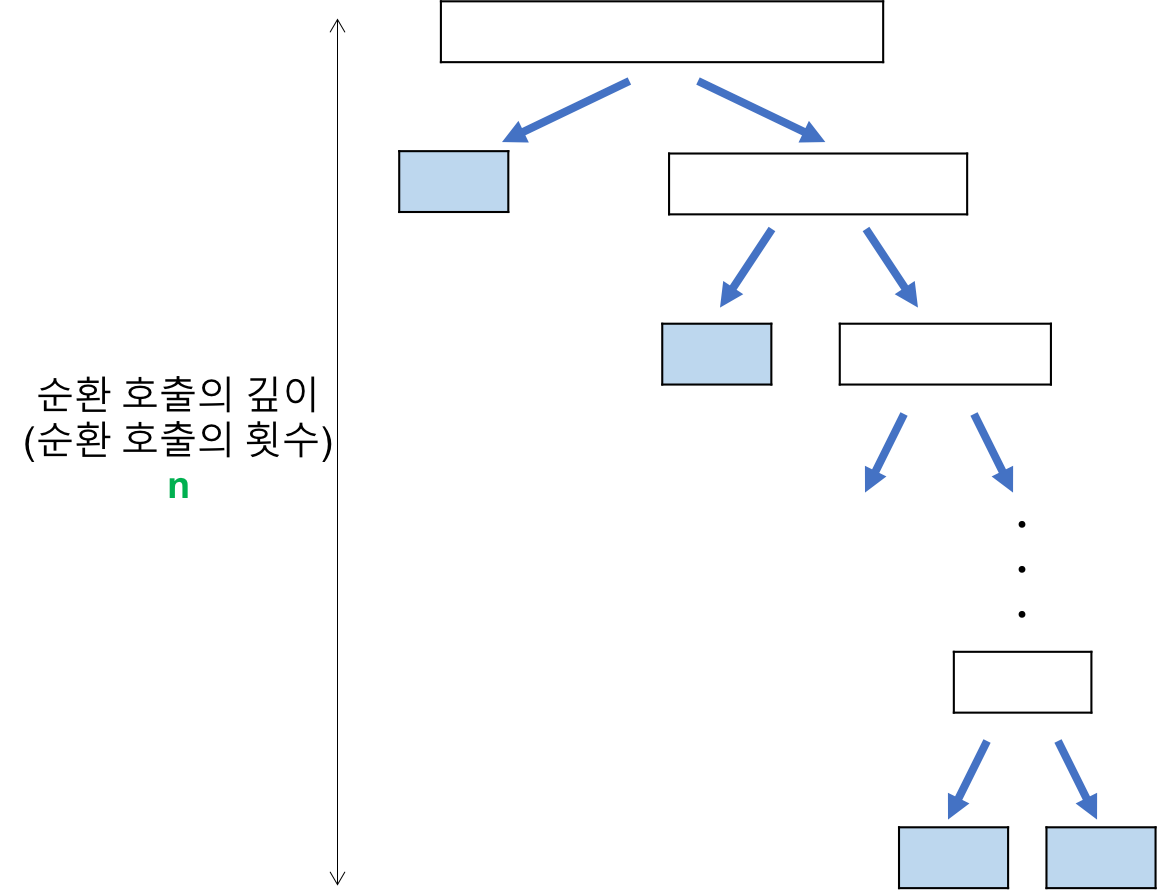
힙 정렬 (Heap sort)

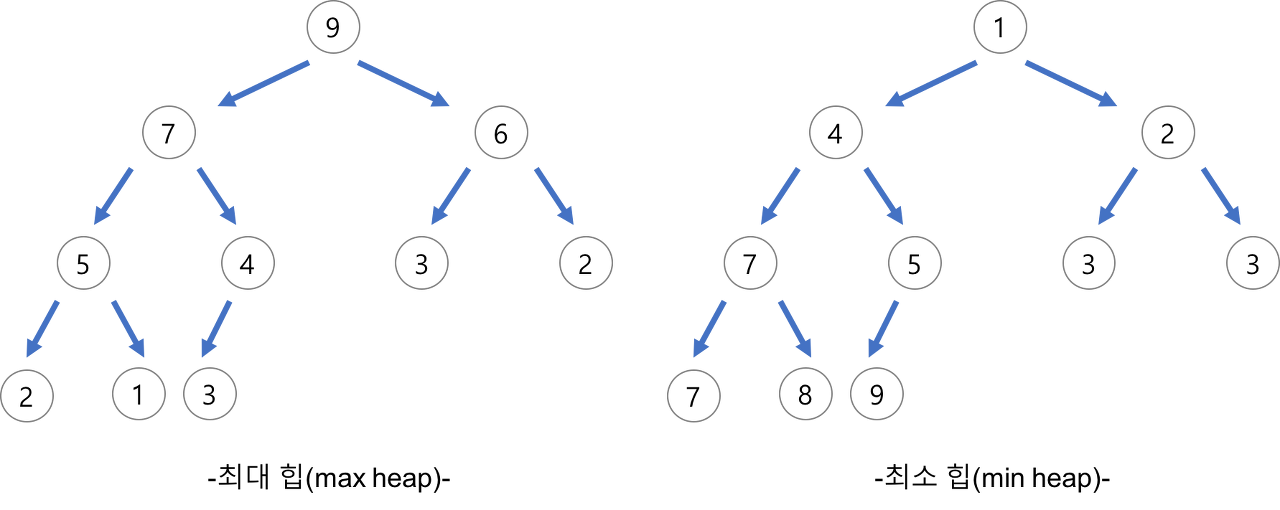
자료구조 '힙'
- 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조
- 최댓값 ,최솟값을 쉽게 추출할 수 있는 자료구조

개념

정렬 알고리즘의 개념요약
- 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법
- 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성하면 됨
- 내림차순 정렬을 위한 최대 힙구현
  - 힙은 2차원 배열로 쉽게 구현될 수 있음
  - 정렬해야 할 n개의 요소들을 1차원 배열에 기억한 후 최대 힙 삽입을 통해 차례대로 삽입
  - 최대 힙으로 구성된 배열에서 최댓값 부터 삭제함

시간복잡도

O(NlogN)

기수 정렬(Radix sort)

개념

비교 정렬을 수행하지 않아 조건이 맞는 상황에서 빠른 정렬 속도를 보장하는 알고리즘
일반적인 정렬법에서 O(NlogN)을 깰수 없다고 알려져 있는데, 이를 깨는 유일한 방법이 기수 정렬
보통 데이터의 낮은 자릿수에서부터 가장 큰 자리수까지 올라가며 정렬을 수행
버킷이라는 별도의 저장 공간에 정렬을 수행하는 중간 단계를 저장하며 진행
위의 이유들로, 자릿수가 존재하지 않는 데이터나 길이가 같지 않은 데이터들을 대상으로는 정렬이 불가능(구현이 불가능 x, 길이가 다를 경우 다른 정렬 알고리즘에 비해 기수 정렬 알고리즘으로 좋은 성능을 내는것은 불가능)
길이가 다른 데이터들을 정렬할 경우 데이터 가공을 위한 별도의 알고리즘이 필요함, 이로 인한 효율의 문제도 고민해보아야 함
기수 정렬의 방식에는 LSD(Least Significant Digit)와 MSD(Most Significant Digit) 두 가지가 존재

LSD

가장 덜 중요한 자릿수 = 가장 작은 자릿수부터 시작해 정렬을 진행

버킷의 크기는 데이터가 한 자릿수에 가질 수 있는 값의 종류에 따라 크기가 정해짐

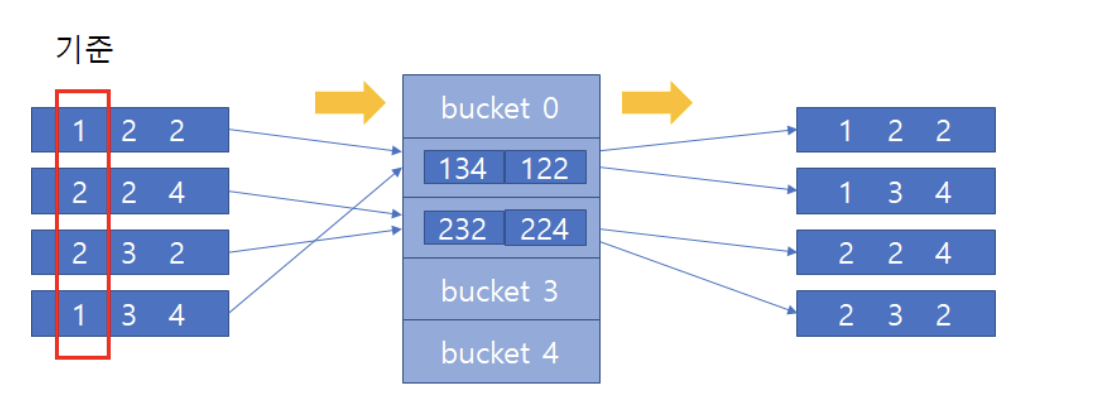
예제에서 다루는 데이터는 5진수이므로 버킷의 크기는 5

1. 첫번째 자릿수를 기준으로 하여 13[4],22[4] 를 순서대로 버킷 4에 넣고

2. 이어서 23[2]와 12[2]를 버킷 2에 넣는다.

3. 그 다음 버킷 0부터 시작해 마지막 버킷 5까지 데이터를 꺼내야 하는데, 하나의 버킷에 둘 이상의 데이터가 존재하는 경우 들어간 순서대로 꺼내면 됨

4. 그러면 232,122,134,224 순으로 데이터가 정렬됨 이제 두번째 자릿수로 넘어감

5. 첫번째 과정과 유일한 차이점은 이번에는 두 번째 자릿수가 정렬의 기준이라는 점

6. 그 외의 모든 과정은 첫번째 과정과 동일

7. 세 번째 과정을 수행함으로 인해 오름차순으로의 정렬이 완료된다.

LSD의 경우 작은 자릿수에서 시작해 가장 큰 자릿수까지 모두 비교를 해야 값의 대소를 판단할 수 있음

MSD

MSD는 가장 중요한 자릿수 = 가장 큰 자릿수부터 시작해서 정렬을 진행함

위 그림은 MSD 방식으로 정렬을 시도했으나 마지막 결과가 우리 예상값과 다르기 때문에 실패한 케이스

왜 MSD는 실패했을까?

224와 232 는 이미 두번째 과정에서 2[2]4 가 2[3]2보다 앞서기 때문에 올바르게 정렬되어 있다고 볼 수 있음
그리고 그 결과는 세번째 자릿수에 영향을 받지 않음
따라서 224와 232는 제자리를 찾았으므로 이 시점에서 정렬을 멈췄어야 함
하지만 여기서 멈추지 않고 세번째 자릿수까지 비교하여 정렬을 진행했기 때문에 잘못된 결과가 초래

이런 오류를 범하지 않으려면 정렬 대상의 일부는 다음 단계로 넘어가되, 일부는 넘어가지 않게 해야함

그래서 MSD 방식에서는 중간에 데이터를 검사해야 함

따라서 구현의 난이도가 LSD에 비해 상대적으로 높아지고 , 중간에 데이터를 검사해야 하므로 성늠의 이점도 반감될 수 있음

이런 이유로 기수 정렬은 일반적으로 LSD 방식을 기준으로 이야기한다.

#include <iostream>
void radix_sort(int a[], int size, int base) {
    int ex, i, j, max = a[0];
    for(i=1; i<size; i++) if(a[i]>max) max=a[i];
    for(ex=1; ex<=max; ex*=base) {
    	int output[size], count[base] = {0};
    	for(i=0; i<size; i++) count[(a[i]/ex)%base]++;
    	for(i=1; i<base; i++) count[i] += count[i-1];
    	for(i=size-1; i>-1; i--) {
    		j = (a[i]/ex)%base;
    		output[count[j]-1] = a[i];
    		count[j]--;
    	}
    	for(i=0; i<size; i++) a[i] = output[i];
    }
}
void radix_sort(int a[], int size) {
    radix_sort(a, size, 10);
}
int main() {
    int arr[] = {9,1,22,4,0,1,22,100,10};
    radix_sort(arr, sizeof(arr)/sizeof(int));
    for(int x: arr) std::cout << x << " ";
    // 0 1 1 4 9 10 22 22 100 
}

데이터의 유형과 길이가 같은 레코드들에 대해서만 수행할 수 있다는 제약 존재
버킷이라는 데이터 전체 크기와 기수 테이블의 크기만큼 추가적인 메모리 필요

시간복잡도

비교 연산을 수행하지 않고 버킷에 데이터를 넣고 빼는 작업(n)을 최대 자릿수(d)만큼 반복하기 때문에 데이터의 개수가 n이고 데이터의 최대 자리수가 d일때 기수정렬의 시간 복잡도는 O(dn)

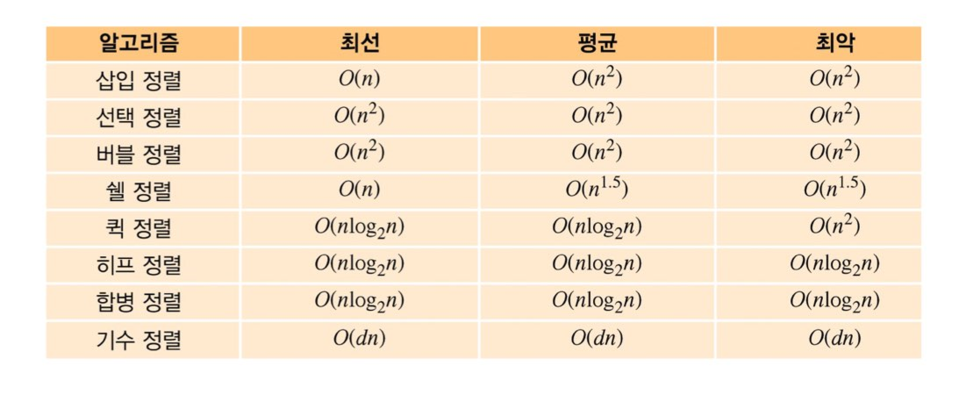
정렬 알고리즘의 시간복잡도 정리

저작자표시 (새창열림)

어제보다 나은 오늘

어제보다 나은 오늘

태그

최근글

댓글

공지사항

아카이브

버블 정렬(Bubble sort)

개념

예시

선택 정렬(Selection sort)

개념

삽입 정렬(Insertion sort)

셸 정렬 (Shell sort)

개념

예시

시간복잡도

합병 정렬 (Merge sort)

개념

예시

시간복잡도

퀵 정렬 (Quick sort)

개념

예시

시간 복잡도

시간복잡도

기수 정렬(Radix sort)

개념

LSD

MSD

시간복잡도

정렬 알고리즘의 시간복잡도 정리

티스토리툴바