[자료구조] Heap
2022. 8. 18. 18:42ㆍCS/자료구조
힙(heap)
- 완전 이진트리의 일종
- 우선순위 큐를 위해 만들어진 자료구조 (우선순위가 높은 데이터가 먼저 나간다!)
- 데이터의 최댓값, 최솟값을 빠르게 찾기 위해 고안된 자료구조
- 반정렬 상태(느슨한 정렬 상태)를 유지한다. → partial order
힙의 종류
- 최대 힙(Max Heap) : 자식 노드의 값이 부모 노드의 값보다 작거나 같음
- 최소 힙(Min Heap) : 부모 노드의 값이 자식 노드의 값보다 작거나 같음

힙의 활용 예시
- 시뮬레이션 시스템
- 네트워크 트래픽 제어
- 운영 체제에서의 작업 스케줄링
- 수치 해석적인 계산
우선순위 큐는 배열, 연결리스트, 힙으로 구현이 가능하다.
이 중에서 힙(heap)으로 구현하는 것이 가장 효율적이다!

힙 구현
- 힙은 배열로 구현
- 주로, 배열의 인덱스 1번을 루트 노드(최상위 부모 노드)로 하고 구현하는 경우가 많다.
- 부모 노드의 인덱스 번호가 n일 때,
- (왼쪽 자식 노드의 인덱스) = 2 * (부모 인덱스)
- (오른쪽 자식 인덱스) = 2 * (부모 인덱스) + 1
- (부모 인덱스) = (자식 인덱스) / 2
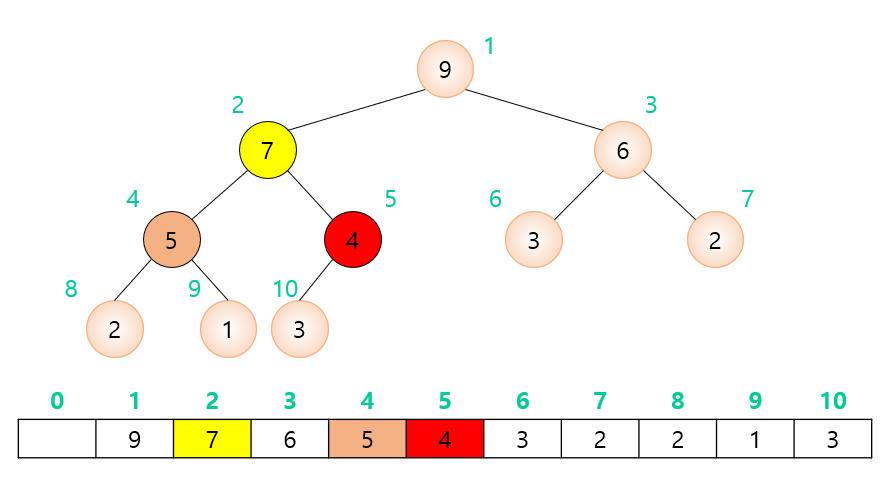
힙의 삽입
- 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 삽입한다.
- 새로운 노드를 부모 노드들과 교환한다.

부모 노드는 자신의 인덱스의 /2 이므로, 비교하고 자신이 더 크면 swap하는 방식이다.
// 최대 힙 삽입
void insert_max_heap(int x) {
maxHeap[++heapSize] = x; // 힙 크기를 하나 증가하고, 마지막 노드에 x를 넣음
for( int i = heapSize; i > 1; i /= 2) {
// 마지막 노드가 자신의 부모 노드보다 크면 swap
if(maxHeap[i/2] < maxHeap[i]) {
swap(i/2, i);
} else {
break;
}
}
}
힙의 삭제
- 최대 힙에서 최대값은 루트 노드이므로 루트 노드가 삭제된다. (최대 힙에서 삭제 연산은 최대값 요소를 삭제하는 것)
- 삭제된 루트 노드에는 힙의 마지막 노드를 가져옴
- 힙을 재구성

// 최대 힙 삭제
int delete_max_heap() {
if (heapSize == 0) // 배열이 비어있으면 리턴
return 0;
int ref = maxHeap[1]; // 루트 노드의 값을 저장
maxHeap[1] = maxHeap[heapSize]; // 마지막 노드 값을 루트로 이동
maxHeap[heapSize--] = 0; // 힙 크기를 하나 줄이고 마지막 노드 0 초기화
for(int i = 1; i*2 <= heapSize;) {
// 마지막 노드가 왼쪽 노드와 오른쪽 노드보다 크면 끝
if(maxHeap[i] > maxHeap[i*2] && maxHeap[i] > maxHeap[i*2+1]) {
break;
}
// 왼쪽 노드가 더 큰 경우, swap
else if (maxHeap[i*2] > maxHeap[i*2+1]) {
swap(i, i*2);
i = i*2;
}
// 오른쪽 노드가 더 큰 경우, swap
else {
swap(i, i*2+1);
i = i*2+1;
}
}
return ref;
}
[출처]
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] Red-Black Tree (0) | 2022.10.07 |
|---|---|
| [자료구조] 이진 탐색 트리 (Binary Search Tree) (0) | 2022.08.18 |
| [자료구조] Hash (0) | 2022.08.18 |
| [자료구조] 배열(Array)과 리스트(List) (0) | 2022.08.16 |